1343. Плохая подстрока

Найдите, сколько существует строк заданной длины n, состоящих только из символов ‘a’, ‘b’ и ‘c’, и не содержащих подстроки “ab”.

Вход. Одно число n (0 ≤ n ≤ 45).

Выход. Выведите количество искомых строк.

Пример входа 1	Пример выхода 1
1	3
Пример входа 2	Пример выхода 2
3	21

РЕШЕНИЕ

рекуррентное соотношение

Анализ алгоритма

Обозначим через f(n) количество искомых строк длины n. При n = 1 таковых имеются 3 строки, при n = 2 имеем 8 строк:

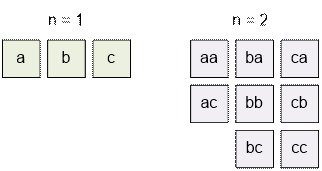
Рассмотрим возможные способы построить требуемые строки. В первой позиции можно поставить одну из трех букв: ‘a’, ‘b’ или ‘c’. Если первой поставить ‘b’ или ‘c’, то в следующих n – 1 позициях можно поставить любое из f(n – 1) слов. Если первой поставить ‘a’, то далее следует рассмотреть случаи расстановки букв во второй позиции. Если во второй позиции поставить ‘c’, то в следующих n – 2 позициях можно поставить любое из f(n – 2) слов. Если во второй позиции поставить ‘a’, то аналогично следует рассмотреть расстановку букв в третьей позиции.

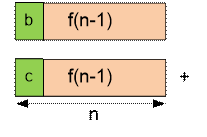
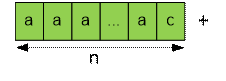
Имеем соотношение:

f(n) = 2f(n – 1) + f(n – 2) + f(n – 3) + … + f(1) + f(0) + 1

Отметим, что в то же время

f(n – 1) = 2f(n – 2) + f(n – 3) + f(n – 4) + … + f(1) + f(0) + 1,

откуда

f(n – 2) + f(n – 3) + f(n – 4) + … + f(1) + f(0) + 1 = f(n – 1) – f(n – 2)

Подставим эту сумму в первое соотношение:

f(n) = 2f(n – 1) + f(n – 1) – f(n – 2) = 3f(n – 1) – f(n – 2)

Таким образом получили рекуррентное соотношение:

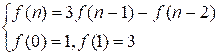
Реализация алгоритма

Значения функции f(i) будем запоминать в ячейках f[i].

#define MAX 46

long long f[MAX];

Вычислим значения f(i) (0 ≤ i ≤ MAX) по приведенной в анализе алгоритма формуле.

f[0] = 1; f[1] = 3;

for(i = 2; i < MAX; i++)

f[i] = 3 * f[i-1] - f[i-2];

Прочитаем входное значение n и выведем результат.

scanf("%d",&n);

printf("%lld\n",f[n]);

Реализация с запоминанием

#include <stdio.h>

#include <string.h>

#define MAX 46

long long m[MAX];

int i, n;

long long f(int n)

{

if (n == 0) return 1;

if (n == 1) return 3;

if (m[n] != -1) return m[n];

return m[n] = 3 * f(n-1) - f(n-2);

}

int main(void)

{

scanf("%d",&n);

memset(m,-1,sizeof(m));

printf("%lld\n",f(n));

return 0;

}

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

long f[] = new long[46];

f[0] = 1; f[1] = 3;

for(int i = 2; i < 46; i++)

f[i] = 3 * f[i-1] - f[i-2];

System.out.println(f[n]);

con.close();

}

}

Java реализация – рекурсия с запоминанием

import java.util.*;

public class Main

{

static long m[] = new long[46];

static long f(int n)

{

if (n == 0) return 1;

if (n == 1) return 3;

if (m[n] != -1) return m[n];

return m[n] = 3 * f(n-1) - f(n-2);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

Arrays.fill(m, -1);

int n = con.nextInt();

System.out.println(f(n));

con.close();

}

}

Python реализация при помощи списка

n = int(input())

res = [1,3]

for i in range(2,46):

res += [3 * res[i-1] - res[i-2]]

print (res[n])

Python реализация при помощи меморизации

res = {0:1,1:3}

def f(n):

if not n in res:

res[n] = 3*f(n-1) - f(n-2)

return res[n]

n = int(input())

print(f(n))